An overview of the Chandra mission and goals, Chandra's namesake, top 10 facts.
Classroom activities, printable materials, interactive games & more.
Overview of X-ray Astronomy and X-ray sources: black holes to galaxy clusters.
All Chandra images released to the public listed by date & by category
Current Chandra press releases, status reports, interviews & biographies.
A collection of multimedia, illustrations & animations, a glossary, FAQ & more.
A collection of illustrations, animations and video.
Chandra discoveries in an audio/video format.
Keep Up With Your Math, and Give Physics A Try Too
December 11, 2002 ::
As part of a class project, a student from Miami, FL, recently sent the
Chandra X-ray Center a series of questions on how trigonometry is used
in astrophysics. Trigonometry is the branch of mathematics that deals
with the relationships between the sides and angles of triangles, and
the calculations based on them. The following text includes replies
from Dr. Patrick Slane, a scientist who uses and works for the Chandra
X-ray Observatory.
My name is Fernando and I live in Miami, Fl. I would like to ask an
Astrophysicist some general questions about how Trigonometry is used in
his/her profession. This is part of a project I am doing for my
Trigonometry class about professions that use Trigonometry.
My name is Pat, and I'm an astrophysicist at the Harvard-Smithsonian
Center for Astrophysics in Cambridge, MA. I study supernova remnants and
neutron stars, both of which are relics of massive star explosions. I
also work on the Chandra X-ray Observatory, helping to plan observations
and operate the spacecraft. I live outside of Boston, MA, where it is
presently quite a bit colder than in Miami, and where the Patriots
currently share the AFC East lead with your Dolphins.
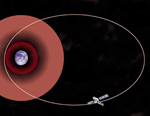
Illustration of Chandra's Orbit |
Would trigonometry be an essential branch of math for someone wanting
to be an astrophysicist?
Absolutely.
Do you use trigonometry very much in your profession?
Yes, and the range of problems for which it is important is vast.
Trigonometry plays a role any time orientation is important. Here are a
couple of examples from my work: using trigonometry to calculate
distances to objects in the Galaxy, figuring out the effects of magnetic
fields on charged particles. (For example, electrons feel a force when
they move perpendicular to a magnetic field, but not parallel to it.
Therefore, it is important to calculate how much of the velocity is
perpendicular to the field.) And, scientists also use trigonometry to
calculate the orbit of a moving spacecraft.
Is trigonometry the kind of math you use most as an astrophysicist or
is there another?
Since math builds so much on previous math, that's a bit hard to say.
For example, you are now studying trigonometry, but I'll bet you are
using more algebra than trigonometry in your work. That is because we
use algebra as tool to make use of the trig. In fact, you probably use
arithmetic even more. It's the same with the work I do. I use calculus
and some other advanced mathematics techniques to do some calculations.
(This will vary from researcher to researcher; someone who works on
theoretical astrophysics will tend to use more calculus, complex
variable analysis, and maybe numerical analysis, than someone who does
more observational and interpretive work, which is what I do.) I use
algebra, trigonometry, and analytic geometry to do lots of calculations
and modeling of data. In the end, I use a ton of arithmetic to put the
numbers together and come up with answers.

Crab Nebula with Scale |
Can you give an example of a problem in astrophysics that can be
solved using trigonometry?
I'll give you a simple one. Let's look at a Chandra image of the Crab
Nebula. This is a bubble of energetic electrons driven as a wind from a
rapidly rotating pulsar (it rotates 30 times a second, has a mass about
1.5 times that of the Sun, and a magnetic field about 1012 - that's ten
to the twelfth power, or 1,000 billion - times stronger than that of the Earth). We believe that the wind forms a circular ring of emission where
it starts to merge with the flow in the rest of the Nebula. You can see
the inner ring in this image, as well as the compact pulsar, as a dot in
the center. The ring certainly doesn't look circular, but we think
that's because it is tilted away from us. You can use Trigonometry to calculate the tilt angle:
- Measure the radius of the long axis of the inner ring, A, and also the
short axis, B. (It doesn't matter what units you use because you are
going to take the ratio of these anyway, and the units will cancel. So
measure it in centimeters on the image, for example.)
- The tilt angle, theta, (or inclination angle, as we call it) is
related to these by cos(theta) = B/A. That is, if theta = 0 (so that the
ring is not tilted at all), we expect B = A, and as theta approaches 90
degrees, the projected size of the short axis approaches zero. The image
indicates that the ring is tilted so that the lower left is farther from
us than the upper right.

Crab Nebula Optical Image |
Too simple? Ok, then consider this: We know from detailed radio and
optical observations that the Crab Pulsar is actually moving across the
sky. For example, pictures taken with the Hubble Space Telescope show
that the pulsar moved about 34.2 milliarcseconds (that's 9.5 millionths
of a degree - quite a telescope that Hubble is!) over the course of 1.9
years. You can use Trigonometry to turn that into an actual speed if you
know the distance, D, to the Nebula. We believe this distance is 2
kiloparsecs (more geometry and trigonometry goes into that definition of
a distance - look it up for extra
credit!) or 6.2 x 1021 cm in more
normal units.
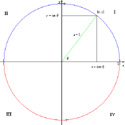 |
- If the angle that the pulsar moves across the sky is phi = 9.5 x 10-6
degrees in that time, that's a distance of d = D*tan(phi). That gives a
velocity of vx = d/t where t = 1.9 years (convert it to seconds). I get
about 170 km/s (yes, I converted it to kilometers - just to make you
work harder!). Note: I called this vx because it is only one component
of the velocity. Keep reading...
 |
Now look back at the image of the Crab Nebula. You can see a jet of
material "spraying" out of the pulsar, directed to the southeast (that's
the lower left in the figure) and the basic form of a counter-jet that
extends in the opposite direction. The interesting thing is that the
direction of the pulsar motion is along that counter-jet direction (that
is, the pulsar is moving toward the upper right in the figure).
What does this have to do with the tilt angle you just calculated? Well,
we assume that the pulsar jet is actually perpendicular to the inner
ring, which means it is tilted into the plane of the sky by the same
tilt angle. The velocity you just calculated is only the component along
the plane of the sky.
That's not the complete velocity because it doesn't include any motion
directly along our line of sight. But you can now calculate it! You have
the x component of the velocity and the angle, so you can get the total
velocity since v
x/v = cos(theta) or v = v
x/cos(theta).
Knowing how fast the pulsar is moving tells us something about the kick
it received when it was formed in a supernova explosion. Knowing that it
is moving along the direction of the jet is presumably telling us
something about the formation of the jet as well. People are still
working on what it all means.
Last exercise: We know the Crab was formed in an explosion in July 1054
A.D., because Chinese astronomers recorded it. How far has it moved from
its birthplace in that time?
By the way, have a look at:
http://chandra.harvard.edu/photo/0052/index.html
for lots more information and images about the Crab.
Do you enjoy using Trigonometry?
I do. It was one of my favorite classes in High School and I still enjoy it.
Out of all six Trigonometric functions, which one is your personal favorite?
I guess that's got to be the tangent because that relates to other
things in spherical geometry (and literature: "This astrophysicist
really seems to have gone off on a tangent about pulsars.").
Which is your least favorite?
Oh, I don't discriminate amongst the rest. I don't really ever use the
secant or cosecant because they are just inverses of the sine and cosine
functions.
When did you last use Trigonometry (before this interview)?
Last Saturday. (That's something else you need to know about
astrophysicists. When we are supposed to be helping to clean the house
on a Saturday morning, sometimes we are squirreled away working on some
calculations instead...)
Keep up with your math, and give physics a try too. Fun stuff.










